一只股票期望与方差怎么求|怎么求期望与方差（方法与步骤），希望说的好理解一些，谢谢！！！！！

一、能不能从未知参数的矩估计量u=E（x）赛格吗²=D（x）中得到它属于正态分布？

这当然是不对的矩估计量u=E(x)，赛格吗²=D(x)只能说明算出来两个值应该是在确定为正态分布之后再计算期望和方差不然不能说明问题

二、设X1，X2，.....Xn是取自N(u，б2)的样本，求样本方差S方的期望和方差

期望其实就是加权平均数，这个样本中每个的权都是一样的，这样的话，期望就是其代数平均数了
Ex=（X1+X2+……+X62）/62
方差的话就是∑（X1-Ex）X（X1-Ex）然后再开平方的结果除以n
一般来说有计算器可以解决的

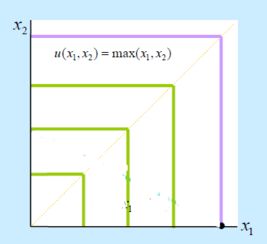
三、X，Y都服从标准正态分布，请问Z=（X^2+Y^2）^0.5的期望是什么啊

1、x1、x2是否相互独立，与你得出的Δ=X1-X2无关。
只与你使用环境有关，与你建模时假设有关，也就是实际情况。
2、如果相互独立，标准正态分布的函数也是标正分布，期望与方差根据公式可求的。
如果不独立，仍然是正态分布，期望与方差需要协方差，建模时如果实际数据，可以进行假设检验，并统计出一个相关系数。
再来求。
这样你的问题角决的就更加科学了。

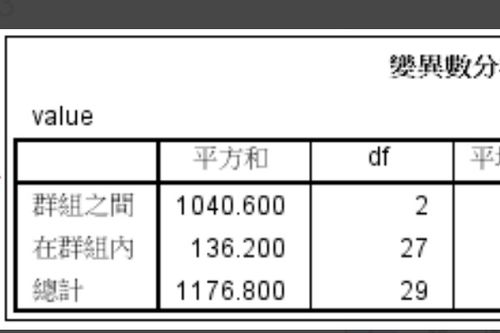
四、谁知道这图标里面的方差怎么算出来的？求助

方差公式：若x1，x2，x3......xn的平均数为m（就是这里的实验组平均值）则方差s^2=1/n[(x1-m)^2+(x2-m)^2+.......+(xn-m)^2]x1  x2  x3……就是实验组里的每个数据。
光看图表算不出来

五、X1，X2分别服从正态分布，那么Y=X1+X2的期望和方差怎么求啊？不是直接吧x1，X2的相加吧？

E(Y)=E(X1)+E(X2).D(Y)就比较复杂了，首先要看他们是否相关，如果X1，X2是相互独立的，那么，D(Y)=D(X1)+D(X2).如果相关则D(Y)=D(X1)+D(X2)+2(E(X1X2)-E(X1)E(X2))

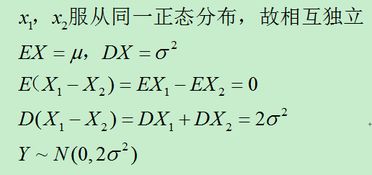
六、怎么求期望与方差（方法与步骤），希望说的好理解一些，谢谢！！！！！

数学期望就是平均值，x_=(x1+x2+x3+……+xn)/n；
方差就是实际值与期望值之差平方的期望值，=[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]/n .

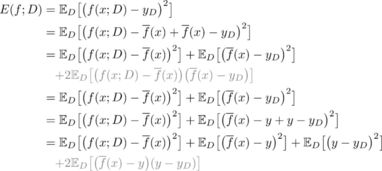
七、X1，X2分别服从正态分布，那么Y=X1+X2的期望和方差怎么求啊？不是直接吧x1，X2的相加吧？

方差是实际值与期望值之差平方的平均值，而标准差是方差平方根。
 在实际计算中，我们用以下公式计算方差。
 方差是各个数据与平均数之差的平方的平均数，即 s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2] ，其中，x_表示样本的平均数，n表示样本的数量，^2表示平方，xn表示个体，而s^2就表示方差。
 而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为总体X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的(n-1)/n倍，[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差，用它作为X的方差的估计具有“无偏性”，所以我们总是用[1/(n-1)]∑(Xi-X~)^2来估计X的方差，并且把它叫做“样本方差”。
 方差，通俗点讲，就是和中心偏离的程度！用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）。
 在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定 。

参考文档