股票哪个指标反映均线离散程度、衡量数据离散程度的指标有哪些

一、衡量数据离散程度的指标有哪些

方差，标准差

二、从哪些指标看到筹码集中度

可以从以下三个指标能够看到筹码集中度。
1.平均数，属于最准确靠谱的指标，用的次数最多。
2.众数，在数字特别多且数大的时候使用。
3.中位数。
碰到有极端数据或模糊不清的数据时使用，使用率与众数差不多。
这是统计概率论里面的知识点。
扩展资料：集中趋势，是指一组数据向某一中心值靠拢的倾向，测度集中趋势也就是要寻找数据一般水平的代表值或中心值。
在现象的同质总体中，各个单位的数量标志值是不尽相同的。
如果我们的目的是要对总体的数量水平有一个概括地、一般地认识，显然是不能用某一单位的数量标志值表示的。
统计平均数就是用来反映总体的一般水平和集中趋势的指标。
通俗的理解就是，在不变更总体总量的情况下，对总体内的全部标志值进行“截长补短”，使得总体各单位拥有同一水平的数量表现，这个同一的数量表现就是平均数，即集中趋势指标。
统计平均数有以下两个重要的特点：1. 平均数是一个代表性值，表示被研究总体的一般水平。
2.平均数把被研究总体的数量标志值在各个单位之间的数量差异抽象化了。
3.利用平均数分析现象之间的相互关系，并推算其它有关的指标。
在统计估算中经常用一部分单位标志值的平均数去推算总体平均数，并据以推算总体的相关总量指标。
例如，在抽样推断中，可以用某县某种农作物产量抽样调查的平均单位面积产量，推断该县农作物的总平均单位面积产量，并据以推算全县某种农作物的总产量。
参考资料：搜狗百科-筹码集中度指标公式

三、描述定量资料离散程度的指标有哪些

描述定量资料离散程度的指标有极差、平均差和标准差。
1、极差极差又称全距，是观测变量的最大取值与最小取值之间的离差，也就是观测变量的最大观测值与最小观测值之间的区间跨度。
极差的计算公式为：R= Max(xi) − Min(xi)2、平均差平均差是总体各单位标志对其算术平均数的离差绝对值的算术平均数。
它综合反映了总体各单位标志值的变动程度。
平均差越大，则表示标志变动度越大，反之则表示标志变动度越小。
3、标准差标准差是随机变量各个取值偏差平方的平均数的算术平方根，是最常用的反映随机变量分布离散程度的指标。
标准差既可以根据样本数据计算，也可以根据观测变量的理论分布计算，分别称为样本标准差和总体标准差。
扩展资料：离散程度的测度意义1、通过对随机变量取值之间离散程度的测定，可以反映各个观测个体之间的差异大小，从而也就可以反映分布中心的指标对各个观测变量值代表性的高低。
2、通过对随机变量取值之间离散程度的测定，可以反映随机变量次数分布密度曲线的瘦俏或矮胖程度。
参考资料来源：百度百科-定量资料参考资料来源：百度百科-离散程度

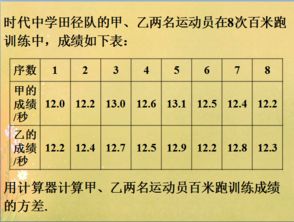
四、股票中什么指标能反映一个趋势的结束和反转？

用高低点和均线配合使用，大波段的高点降低,低点突破前一个波段的低点,代表趋势终结.此时均线可能尚未空头排列,就如这两天的大盘，突破均线后会反抽等待均线的调整到位.注意大波段和小波段的关系,还要注意震荡市场不能用趋势判断方法.3478-3361两个顶降低，但2639-2890低在抬高,这是震荡市的表现.大盘目前大趋势是震荡，3361后的中期趋势是下降.可以参考万科,联通的大趋势走坏.

五、什么是离散指标?离散指标有什么作用?

可用来测度观测变量值之间差异程度的指标有很多，在统计分析推断中最常用的主要有极差、平均差和标准差等几种。
1、极差极差又称全距，是观测变量的最大取值与最小取值之间的离差，也就是观测变量的最大观测值与最小观测值之间的区间跨度。
极差的计算公式为：r= max(xi) − min(xi)2、平均差平均差是总体各单位标志对其算术平均数的离差绝对值的算术平均数。
它综合反映了总体各单位标志值的变动程度。
平均差越大，则表示标志变动度越大，反之则表示标志变动度越小。
3、标准差标准差是随机变量各个取值偏差平方的平均数的算术平方根，是最常用的反映随机变量分布离散程度的指标。
标准差既可以根据样本数据计算，也可以根据观测变量的理论分布计算，分别称为样本标准差和总体标准差。
标准差是一组数值自平均值分散开来的程度的一种测量观念。
一个较大的标准差，代表大部分的数值和其平均值之间差异较大；
一个较小的标准差，代表这些数值较接近平均值。
例如，两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ，但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。
例如在物理科学中，做重复性测量时，测量数值集合的标准差代表这些测量的精确度。
当要决定测量值是否符合预测值，测量值的标准差占有决定性重要角色：如果测量平均值与预测值相差太远（同时与标准差数值做比较），则认为测量值与预测值互相矛盾。
这很容易理解，因为值都落在一定数值范围之外，可以合理推论预测值是否正确。

参考文档