研究样本量的比例是什么意思~什么是比？什么是比例

一、样本比例的定义是什么

研究中实际观测或调查的一部分个体称为样本。
研究对象的全部称为总体。
为了使样本能够正确反映总体情况，对总体要有明确的规定；
总体内所有观察单位必须是同质的；
在抽取样本的过程中，必须遵守随机化原则；
样本的观察单位还要有足够的数量。
又称“子样”。
按照一定的抽样规则从总体中取出的一部分个体。
样本中个体的数目称为“样本容量”。

二、市场调查的抽样调查样本量公式n= Z2σ2/e2 和n= Z2P(1-P)/e2的区别还有σ代表什么

1．简单随机抽样确定样本量主要有两种类型：

 　　（1）对于平均数类型的变量

　　对于已知数据为绝对数，我们一般根据下列步骤来计算所需要的样本量。
已知期望调查结果的精度(E)， 期望调查结果的置信度(L)，以及总体的标准差估计值σ的具体数据，总体单位数N。
 

计算公式为：n=σ2/(e2/Z2+σ2/N) 

特殊情况下，如果是很大总体，计算公式变为：n= Z2σ2/e2 

例如希望平均收入的误差在正负人民币30元之间，调查结果在95%的置信范围以内，其95%的置信度要求Z的统计量为1.96。
根据估计总体的标准差为150元，总体单位数为1000。
 

样本量：n=150*150/(30*30/(1.96*1.96))+150*150/1000)=88 

(2)于百分比类型的变量 

对于已知数据为百分比，一般根据下列步骤计算样本量。
已知调查结果的精度值百分比(E)，以及置信度(L)，比例估计(P)的精度，即样本变异程度，总体数为N。
 

则计算公式为：n=P(1-P)/(e2/Z2+ P(1-P)/N) 

同样，特殊情况下如果不考虑总体，公式为：n= Z2P(1-P)/e2   

一般情况下，我们不知道P的取值，取其样本变异程度最大时的值为0.5。
 

例如：希望平均收入的误差在正负0.05之间，调查结果在95%的置信范围以内，其95%的置信度要求Z的统计量为1.96，估计P为0.5，总体单位数为1000。
样本量为：n=0.5*0.5/(0.05*0.05/(1.96*1.96)+0.5*0.5/1000)=278

三、不同总体量和样本量时如何计算比例的置信区间 详细

总体，样本量，置信区间 在总体或者总体子集不大情况下的抽样调查中，往往不易得出合理的关于比例的区间估计。
这一类问题在抽样调查实践中已经严重到非说不可的地步。
文章讨论了在样本量不大或者(和)在总体不大时估计比例的置信区间时往往忽略的问题，并给出了在不同情况下如何计算置信区间的方法。
 不同总体量和样本量时如何计算比例的置信区间

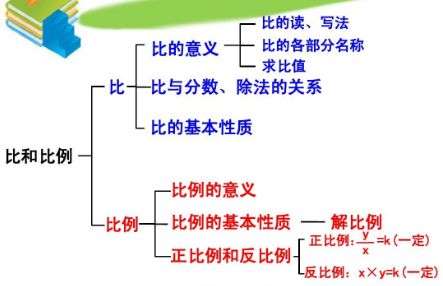
四、比和比例是什么意思？

比和比例　　比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括： 　　比，等同于算式中等号左边的式子，是式子的一种（如：a：b）；
 　　比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a：b=c：d）。
 　　所以，比和比例的联系就可以说成是： 　　比是比例的一部分；
而比例是由至少两个比值相等的比组合而成的. 　　表示两个比相等的式子叫做比例，是比的意义 　　比例有4项，前项后项各2个. 　　在比例里，两个外项的即等于两个内项的积，这叫做比的基本性质. 　　比表示两个数相除；
只有两个项：比的前项和后项。
 比例是一个等式，表示两个比相等；
有四个项：两个外项和两个内项。
比的性质： 比的前项和后项都乘以或除以一个不为零的数。
比值不变。
 比的性质用于化简比。
比例的性质：在比例里，两个外项的乘积等于两个内项的乘积。
比例的性质用于解比例。
 　　比和比例 　　比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括： 　　比，等同于算式中等号左边的式子，是式子的一种（如：a：b）；
 　　比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a：b=c：d）。
 　　所以，比和比例的联系就可以说成是： 　　比是比例的一部分；
而比例是由至少两个比值相等的比组合而成的.区别　　区别1：意义、项数、各部分名称不同。
比表示两个数相除；
只有两个项：比的前项和后项。
 如：a：b 这是比 比例是一个等式，表示两个比相等；
有四个项：两个外项和两个内项。
 a：b=3：4 这是比例。
 　　区别2：比的基本性质和比例的基本性质意义不同、应用不同。
比的性质： 比的前项和后项都乘或除以一个不为零的数。
比值不变。
比例的性质：在比例里，两个外项的乘积等于两个内项的乘积相等。
 比例的性质用于解比例。
联系： 比例是由两个相等的比组成。
比和比例的意义　　比的意义是两个数的除又叫做两个数的比，而比例的意义是表示两个比相等的式子是叫做比例。
比是表示两个数相除，有两项；
比例是一个等式，表示两个比相等，有四项。
因此，比和比例的意义也有所不同。
 而且，比号没有括号的含义 而另一种形式，分数有括号的含义！ 　　比和比例既有联系，又有区别。
 联系：比和比例有着密切联系。
 比是研究两个量之间的关系，所以它有两项；
比例是研究相关联的两种量中两组相对应数的关系，所以比例是由四项组成。
 比例是由比组成的，如果没有两种量的比，比例就不会存在。
比例是比的发展，如果把比例式中右边的比看成一个数，比和比例此时又可以统一起来。
 如果两个比相等，那么这两个比就可以组成比例。
成比例的两个比的比值一定相等。
 区别： 比和比例的区别用表说明。
 意 义 形 式 组 成 比 比是表示两个数相除的关系 比由两项组成（前项、后项） 任意两个数都能组成比 比例 比例是表示两个比相等 的关系 比例由四项组成（两个内 项、两个外项） 任意四个数不一定都能组成比例 正比例与反比例的相同点与不同点 相同点 不同点 关系式 正比例 两种相关联的量，一种量随着另一种量的变化而变化 相对应的两个量的比值（商）一定 （一 定） 反比例 两种相关联的量，一 种量随着另一种量的变化而变化。
 相对应的两个量的积一定 xy=k (一定)

五、什么是比？什么是比例

关于比：    （1）比的意义：两个数相除又叫做两个数的比。
      （2）部位名称：“：”是比号，读作“比”。
比号前面的数叫做比的前项，比号后面的数叫做比的后项。
比的前项除以后项所得的商，叫做比值。
       如：20 （前项）：（比号） 50（后项）＝20÷50＝2/5（比值）     （3）与除法、分数比较：      同除法比较，比的前项相当于被除数，比号相当于÷（除号），后项相当于除数，比值相当于商。
      同分数比较，比的前项相当于分子，比号相当于/（分数线），后项相当于分母，比值相当于分数的值。
     （4）基本性质：比的前项和后项同时乘上或者同时除以相同的数（0除外），比值不变。
    关于比例：    比例，技术制图中的一般规定术语，是指图中图形与其实物相应要素的线性尺寸之比。
   ①表示两个比相等的式子叫做比例，如3：4＝9：12.在3：4＝9：12中，其中3与12叫做比例的外项，4与9叫做比例的内项。
比例有四个项，分别是两个内项和两个外项。
  ②比例，如：教师和学生的比例已经达到要求。
  ③比重，如：在所销商品中，国货的比重比较大。
  ④比例写成分数的形式后，那么，左边的分母和右边的分子是内项，左边的分子和右边的分母是外项。
  ⑤在一个比例中，两个外项的积等于两个内项的积，这叫做比例的基本性质。
   比例是一个总体中各个部分的数量占总体数量的比重，用于反映总体的构成或者结构。
    比例分为比例尺和比例. 表示两个比相等的式子叫做比例。
判断两个比能不能组成比例，要看它们的比值是不是相等。
组成比例的四个数，叫做比例的项。
两端的两项叫做比例的外项，中间的两项叫做比例的内项。
在比例里，两个外项的积等于两个内项的积。
求比例的未知项，叫做解比例。
     比如：x：3= 9：27    解法   x：3=9：27    解：27x=3×9           27x=27              x=1

六、：比例是什么意思

1 表示两个比相等的式子：如 3：4=9：122两个同类量之间的倍数关系。
如 教师和学生的比例已经达到要求3 比重。
 如 在所销商品中，国货的比重比较大。

七、不明白抽样比是什么意思 哪位大神解释一下

比和比例　　比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括： 　　比，等同于算式中等号左边的式子，是式子的一种（如：a：b）；
 　　比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a：b=c：d）。
 　　所以，比和比例的联系就可以说成是： 　　比是比例的一部分；
而比例是由至少两个比值相等的比组合而成的. 　　表示两个比相等的式子叫做比例，是比的意义 　　比例有4项，前项后项各2个. 　　在比例里，两个外项的即等于两个内项的积，这叫做比的基本性质. 　　比表示两个数相除；
只有两个项：比的前项和后项。
 比例是一个等式，表示两个比相等；
有四个项：两个外项和两个内项。
比的性质： 比的前项和后项都乘以或除以一个不为零的数。
比值不变。
 比的性质用于化简比。
比例的性质：在比例里，两个外项的乘积等于两个内项的乘积。
比例的性质用于解比例。
 　　比和比例 　　比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括： 　　比，等同于算式中等号左边的式子，是式子的一种（如：a：b）；
 　　比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a：b=c：d）。
 　　所以，比和比例的联系就可以说成是： 　　比是比例的一部分；
而比例是由至少两个比值相等的比组合而成的.区别　　区别1：意义、项数、各部分名称不同。
比表示两个数相除；
只有两个项：比的前项和后项。
 如：a：b 这是比 比例是一个等式，表示两个比相等；
有四个项：两个外项和两个内项。
 a：b=3：4 这是比例。
 　　区别2：比的基本性质和比例的基本性质意义不同、应用不同。
比的性质： 比的前项和后项都乘或除以一个不为零的数。
比值不变。
比例的性质：在比例里，两个外项的乘积等于两个内项的乘积相等。
 比例的性质用于解比例。
联系： 比例是由两个相等的比组成。
比和比例的意义　　比的意义是两个数的除又叫做两个数的比，而比例的意义是表示两个比相等的式子是叫做比例。
比是表示两个数相除，有两项；
比例是一个等式，表示两个比相等，有四项。
因此，比和比例的意义也有所不同。
 而且，比号没有括号的含义 而另一种形式，分数有括号的含义！ 　　比和比例既有联系，又有区别。
 联系：比和比例有着密切联系。
 比是研究两个量之间的关系，所以它有两项；
比例是研究相关联的两种量中两组相对应数的关系，所以比例是由四项组成。
 比例是由比组成的，如果没有两种量的比，比例就不会存在。
比例是比的发展，如果把比例式中右边的比看成一个数，比和比例此时又可以统一起来。
 如果两个比相等，那么这两个比就可以组成比例。
成比例的两个比的比值一定相等。
 区别： 比和比例的区别用表说明。
 意 义 形 式 组 成 比 比是表示两个数相除的关系 比由两项组成（前项、后项） 任意两个数都能组成比 比例 比例是表示两个比相等 的关系 比例由四项组成（两个内 项、两个外项） 任意四个数不一定都能组成比例 正比例与反比例的相同点与不同点 相同点 不同点 关系式 正比例 两种相关联的量，一种量随着另一种量的变化而变化 相对应的两个量的比值（商）一定 （一 定） 反比例 两种相关联的量，一 种量随着另一种量的变化而变化。
 相对应的两个量的积一定 xy=k (一定)

八、样本含量什么意思

样本含量估计充分反映了科研设计中“重复”的基本原则，过小过大都有其弊端。
样本含量过小，所得指标不稳定，用以推断总体的精确度（包括精密度和准确度）差；
检验效能1-低，使应有的差别不能显示出来，难以获得正确的研究结果，结论也缺乏充分的依据。

参考文档