股票上涨数学期望值怎么看；数学期望值是什么

一、股票经常说上涨多少个点了，这一点是怎么算的？怎么看的？

简单的数学运算啊，比如说某股票昨天收盘价是10元，今天中午收盘是10.5元，下午收盘是11元，那分别是上涨了5个点和10个点。
(10.5-10)/10=0.05 即5% (11-10)/10=0.1 即10%

二、如何确定某种股票的期望报酬率

假定投资者将无风险的资产和一个风险证券组合再构成一个新的证券组合，投资者可以在资本市场上将以不变的无风险的资产报酬率借入或贷出资金。
在这种情况下，如何计算新的证券组合的期望报酬率和标准差？假设投资于风险证券组合的比例（投资风险证券组合的资金/自有资金）为Q，那么1-Q为投资于无风险资产的比例。
无风险资产报酬率和标准差分别用r无 、σ无 表示，风险证券组合报酬率和标准差分别用r风 、σ风 表示，因为无风险资产报酬率是不变的，所以其标准差应等于0，而无风险的报酬率和风险证券组合的报酬率不存在相关性，即相关系数等于0。
那么新的证券组合的期望报酬率和标准差公式分别为： rP = Qr风 +（1-Q）r无

三、有关数学题中股票涨跌值的问题

股票上升与下降的数据是代表什么啊？比如说：-0.10，➕0.45之类的。
这是代表每股价格的百分之几还是什么咧？再比如说“周三的收盘价是多少？本周内每股最高价是多少元？”收盘价是什么？最高价是算哪里的？问题一：股票上升与下降的数据（即股价上涨幅度）是代表该股今天股价相对前一交易日收盘价上涨或下跌的百分比。
股价上涨幅度=（目前股价-前一交易日收盘价）/前一交易日收盘价。
问题二：收盘价是指某种证券在证券交易所一天交易活动结束前最后一笔交易的成交价格。
目前沪深股市的收盘价并不完全是最后一笔交易的成交价格，而是一个加权平均价，也叫已调整收盘价。
 上海证券交易所交易规则规定沪市收盘价为当日该证券最后一笔交易前一分钟所有交易的成交量加权平均价（含最后一笔交易）。
深圳证券交易所交易规则规定深市证券的收盘价通过集合竞价的方式产生。
收盘集合竞价不能产生收盘价的，以当日该证券最后一笔交易前一分钟所有交易的成交量加权平均价(含最后一笔交易)为收盘价。
当日无成交的，沪深以前收盘价为当日收盘价。
问题三：本周内每股最高价是指该股一周内（所有交易日）的最高成交价。
比如某股，周一最高成交价是10.2，周二最高成交价是10.8，周三最高成交价是10.5，周四最高成交价是11.3，周五最高成交价是11.2，那么该股本周最高价是11.3元。

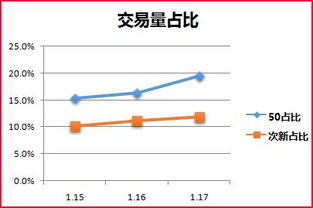
四、数学期望值是什么

在概率和统计学中，一个随机变量的期望值（或期待值）是变量的输出值乘以其机率的总和，换句话说，期望值是该变量输出值的平均数。
期望值并不一定包含于变量的输出值集合里。
例如，美国赌场中经常用的轮盘上有38个数字，每一个数字被选中的几率都是相等的。
赌注一般压在其中某一个数字上，如果轮盘的输出值和这个数字相等，那么下赌者可以将相当于赌注35倍的奖金和原赌注拿回（总共是原赌注的36倍），若输出值和下压数字不同，则赌注就输掉了。
因此，如果赌注是1美元的话，这场赌博的期望值是：( -1 × 37/38 ) + ( 35 × 1/38 )， 结果是 -0.0526。
也就是说，平均起来每赌一次就会输掉5美分。
数学定义如果X是在机率空间(Ω， P)中的一个随机变量，那么它的期望值 E(X) 的定义是： E(X)=∫ΩXdp并不是每一个随机变量都有期望值的，因为有的时候这个积分不存在。
如果两个随机变量的分布相同，则它们的期望值也相同。
如果 X 是一个离散的随机变量，输出值为 x1， x2， ...， 和输出值相应的机率为p1， p2， ... （机率和为1）， 那么期望值 E(X) 是一个无限数列的和。
上面赌博的例子就是用这种方法求出期望值的。
如果X的机率分布存在一个相应的机率密度函数 f(x)，那幺 X 的期望值可以计算为：这种算法是针对于连续的随机变量的，与离散随机变量的期望值的算法同出一辙，由于输出值是连续的，所以把求和改成了积分。
特性期望值 E 是一个线形函数 X 和 Y 为在同一机率空间的两个随机变量，a 和 b 为任意实数。
 一般的说，一个随机变量的函数的期望值并不等于这个随机变量的期望值的函数。
 在一般情况下，两个随机变量的积的期望值不等于这两个随机变量的期望值的积。
特殊情况是当这两个随机变量是相互独立的时候（也就是说一个随机变量的输出不会影响另一个随机变量的输出）。
 期望值的运用在统计学中，当估算一个变量的期望值时，一个经常用到的方法是重复测量此变量的值，然后用所得数据的平均值来作为此变量的期望值的估计。
在概率分布中，期望值和方差或标准差是一种分布的重要特征。
在经典力学中，物体重心的算法与期望值的算法十分近似

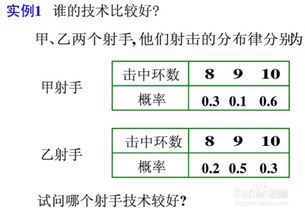
五、数学期望值是什么，怎么计算

随机变量分别和它对应的概率相乘，然后再相加即（1*1/6）+（2*1/3）+（3*1/3）+（4*1/6）

六、怎么判断一个变量是否存在数学期望

根据定义：对于离散变量：数学期望是每个概率和对应的值的积的和：E(X)=x1p1+...+XnPn对于连续变量：E(X)=integral i-n (XiPi)变量存在它对应的数学期望：当然得有一个样本，并且对于样本中的每个值都要有一个概率.这样才能根据公式算出这个样本的变量的期望值.

参考文档