期权vega值是什么意思.期权含义

一、vega值的实际应用

如果某期权的Vega为0.15，若价格波动率上升（下降）1%，期权的价值将上升（下降）0.15。
若期货价格波动率为20%，期权理论价值为3.25，当波动率上升为22%，期权理论价值为 3.55（3.25+2×0.15）；
当波动率下为18%，期权理论价值为2.95（3.25-2×0.15）。
当价格波动率增加或减少时，期权的价值都会增加或减少因此，看涨期权与看跌期权的Vega都是正数。
期权多头部位的Vega都是正数， 期权空头的Vega都是负数。
如果投资者的部位Vega值为正数，将会从价格波动率的上涨中获利，反之，则希望价格波动率下降。
对于Delta中性的部位，就可以不受期货价格的影响，而从价格波动率的变化中寻找盈利机会。
对于外汇期权的买方而言，Vega值始终大于零，说明标的汇率波动性的增加将提高外汇期权的价值；
相反，对于外汇期权的卖方而言，其Vega值始终为负。
同样，当外汇期权处于平价状态时，Vega值最大；
当期权处于较深的价内或者价外时，Vega值接近于零。

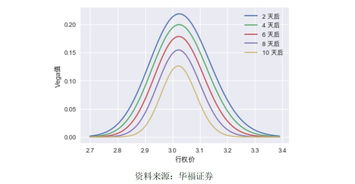
二、vega值的简介

Vega值--认股证对引伸波幅变动的敏感度，它反映当引伸波幅变化一个单位时，认股证价格理论上的变化，Vega值永远都是正数，值越大，投资者面对引申波幅变化的风险便越大。
期权波幅每1%的改变会造成其价若干的变动，也称Vega值。
 期权的风险指标通常用希腊字母来表示，包括：delta值、gamma值、theta值、vega值、rho值等。
Vega（ν）：衡量标的资产价格波动率变动时，期权价格的变化幅度，是用来衡量期货价格的波动率的变化对期权价值的影响。
Vega，指期权费（P）变化与标的汇率波动性（Volatility）变化的敏感性。
公式为：Vega=期权价格变化/波动率的变化。

三、期权是什么意思？工作中的期权指什么？

期权是一种对职工的鼓励政策。
也有的是对要离职员工的挽留政策。
 
会根据一定的规则来制定每份期权的价格，有的需要自己买，有的是公司作为福利赠送，相当于股票似地，假如开始发给你的时候是1元钱1股，你有10股。
如果公司发展的好，变成了100块钱一股，那你就赚了。
 但是，如果公司发展得不好，那么期权也没有什么意义。

四、求~期权公式代码含义

欧式看涨期权公式：
C=SN(d)-Le-rtN(d-σ t)
式中C为叫买期权的价值；
S为现在股价；

N(d)为变量d的标准正态分布函数（偏差小于d的概率）；
L为敲定价格（也叫执行价格或履约价格）；
e为自然对数的底，等于2.71828…；
r为无风险利率；
t为期权到期的时间；

N(d-σ t)为函数；
d为一变量，
S σ2
d=Ln — + (r+ — )t
L 2
其中Ln为自然对数；

σ为股价波动的标准差。

公式中叫买期权的价值为两部分之差。
公式右边第一项为期望的股价，公式右边第二项为股票期望的成本。
即价值为期望股价与期望成本之差。
公式表明，今日股价S愈高，则叫买期权价C愈高。
股价的波动愈大（用标准偏差测量），则期权价值越高。
期权到期的时间t愈长，敲定价L愈低，期权执行的可能性就更大（这种可能性由正态分布函数来估定）。

五、期权是什么意思？

期权又称为选择权，是一种衍生性金融工具。
是指买方向卖方支付期权费(指权利金)后拥有的在未来一段时间内(指美式期权)或未来某一特定日期(指欧式期权)以事先规定好的价格(指履约价格)向卖方购买或出售一定数量的特定商品的权利，但不负有必须买进或卖出的义务。
期权特性具有"零和游戏"特性，而个股期权及指数期权皆可组合，进行套利交易或避险交易。
期权主要可分为买方期权(Call Option)和卖方期权(Put Option)，前者也称为看涨期权或认购期权，后者也称为看空期权或认沽期权。
具体分为四种：1.买入买权(long call) 2.卖出买权( short call) 3. 买入卖权(long put) 4.卖出卖权(short put)期权交易事实上是这种权利的交易。
买方有执行的权利也有不执行的权利，完全可以灵活选择。
 期权分场外期权和场内期权。
场外期权交易一般由交易双方共同达成。

六、股票期权中Delta的含义是什么？

什么是Delta值？Delta值是什么意思？不少权证投资者都听说过对冲值（Delta）概念，但大都对这个概念还不十分熟悉，缺乏清晰的认识。
Delta值，亦称为对冲比率，是一种可以显示相关资产价格变动时对期权价格影响的变动率。
认购期权的Delta 值为正数(范围在0和+1之间)，因为股价上升时，认购期权的价格也会上升。
认沽期权的Delta值为负数(范围在-1和0之间)，因为股价上升时，认沽期权的价格即会下降。
等价认购期权之Delta值会接近0.5，而等价认沽期权的则接近-0.5。
对冲值表示的是权证价格变化对正股价格变化的敏感度，也就是说，当正股价格变动1元时理论上权证价格的变动量。
在数值上，对冲值等于权证价格变动量除以正股价格的变动量。
对冲值还反映到期时权证成为价内的概率。
权证的对冲值还可以用来计算权证的有效杠杆比率。
例如，汇丰控股（005）150元认购期权的Delta值等于0.5元，即表示汇丰控股股价上升1元时，认购期权价格将随而上升0.5元。
同样地，若果一个汇丰控股认沽期权的Delta数值是-0.4时，表示当汇丰控股价格上升1元时，期权金就会下跌0.4元。
但投资者亦请注意，期权的Delta值会随股价大幅变动而有所改变，有关Delta值预期对期权金之影响的变动率只适用于正股价出现轻微变动的时候。
因此当股价出现大幅变动时，便不应使用Delta值来预测期权价格的变动。
期权庄家在市场提供流通量(即负责开出某期权系列的买卖价)时，若市场出现买卖对手后，他便会在该合约持有仓位。
例如当对手向他买入一张认购期权合约，便等如他持有该认购期权的短仓。
但因为通常他作为庄家的目的并非与对手对赌，故此他便需要为持仓作对冲。
此时他便要�定需买入多少正股(因为持有认购短仓的风险是股价上升)作对冲之用，当中Delta便是其中一项帮助他计算对冲正股数目的风险夒数。
假设该庄家持有的认购期权短仓之Delta值为-0.5，若要为持仓进行Delta Neutral(Delta中性)对冲，便需买入Delta值为+0.5的股票。
换句话说，他必须为每2手期权买入1手正股(因正股之Delta值为+1)作对冲。
当然，如前述Delta值会随股价变动而会不断改变，故此等对冲必须时刻作调整。
如当正股价格上升后，该认购期权之Delta值亦上升，需买入之正股数量亦需向上调整。
相反，若正股价格下跌，该认购期权之Delta值便会下跌，需买入之正股数量亦需相应减少。
另外，投资者在持有期权组合时，必须明了其Delta值是相等于所有组成期权系列之总和。
而Delta值非一个常数，它的数值是在-1至+1之间，实际的Delta值亦会因应相关资产，波幅、息率及距离到期日时间等因素而有所改变，所以当投资者买入或沽出期权合约后，必须不断密切留意持有期权组合的整体Delta值变化，在需要对冲时根据其变化而调整正股数目，避免过度对冲或未有完全对冲。

七、期权含义

期权（option；
option contract）又称为选择权，是在期货的基础上产生的一种衍生性金融工具。
从其本质上讲，期权实质上是在金融领域中将权利和义务分开进行定价，使得权利的受让人在规定时间内对于是否进行交易，行使其权利，而义务方必须履行。
在期权的交易时，购买期权的一方称作买方，而出售期权的一方则叫做卖方；
买方即是权利的受让人，而卖方则是必须履行买方行使权利的义务人。

八、如何引用期权的隐含波动率

隐含波动率，作为期权市场的特有信息，表达了对市场未来波动状况的预期，对于上证50ETF期权而言，它是目前国内上市时间最长、成交最为活跃的期权品种，通过分析其隐含波动率，对于理解市场情绪、研判标的价格走势有一定的指示意义。
隐含波动率指数的构建单一合约隐含波动率的计算很简单，由期权价格反推而得，但是期权合约众多，每一个合约的隐含波动率只能反映该合约的性质，对于整个期权市场则缺乏有效指引。
研究者会根据各个期权合约的实虚值状态、成交量大小、期权存续期等因素，计算出某一日的综合隐含波动率，并按日期连线得到隐含波动率指数曲线，以此来反映市场状况。
一般来说，有以下四类隐含波动率指数编制方法：一是VIX指数编制方法。
该方法由美国CBOE交易所首次提出，利用方差互换原理，通过选取近月合约和次近月合约一系列满足条件的看涨、看跌期权的隐含波动率，将其加权平均而得。
二是交易量加权法。
其权重是该品种期权交易量与该期权总交易量的比值，显然，成交量越大的品种对整体隐含波动率产生的影响越大。
三是Vega加权法。
Vega是指期权价格相对于标的资产波动的敏感系数。
由期权定价理论可知，平值期权的Vega值最大。
从市场表现看，平值期权也是成交最为活跃的一类合约，该加权方式和成交量加权法类似。
四是特定合约选取法。
不进行加权，只选取代表性期权合约隐含波动率，例如，平值期权、成交量最大期权合约等。
事实上，无论哪种方法，得到的隐含波动率走势差别不大。
下面按照特定合约选取方式，计算近月合约平值看涨、看跌期权算术平均隐含波动率，将其作为波动率代表，得到波动率指数如图IVIX与近月平值隐含波动率所示。

参考文档