股票的贝塔系数怎么找-如何查看单个股票每年的β系数，求教详细过程，诚心感谢了

一、已知、tanα=1/2 、tanβ=1/3 、0<α<2π、π<β<3/2π、求α+β的值

tanα=1/2 、tanβ=1/3 tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)=(1/2+1/3)/(1-1/2*1/3)=10<α<2π、π<β<3/2πtanα=1/2 、tanβ=1/3可看出：π<α<3π/2或0<α<π/22π<α+β<3π或π<α+β<2π因为tan(α+β)=1所以：α+β=5π/4或9π/4

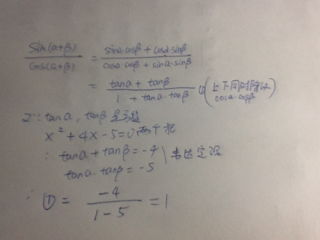
二、如何解释一只股票的Beta值接近于1

贝塔系数衡量股票收益相对于业绩评价基准收益的总体波动性，是一个相对指标。
 β 越高，意味着股票相对于业绩评价基准的波动性越大。
 β 大于 1 ，则股票的波动性大于业绩评价基准的波动性。
反之亦然。
 详见股票百科

三、上市公司的股权成本和贝塔值在哪里可以查到？（免费）

股权成本是要算的。
。
。
用市盈率也可以，不一定非要用贝塔值。
股权成本=市场股利支付比率*（1+盈余增长率）/市盈率中位数+盈余增长率至于贝塔值你看一下股票行情软件里的F10，不一定有，国内股市还没有国外那么健全。
。
。

四、如何查看单个股票每年的β系数，求教详细过程，诚心感谢了

各个股票风险不同，比如银行股风险就比较小，取大盘平均风险系数为1，那某股票相对于大盘的风险系数就是贝塔系数，风险比大盘小，系数就小于1，反之，则大于1

五、财务管理问题：某公司持有ABC三种股票构成的证券组合，β系数分别为2.0、1.0和0.5

这种情况不应投资。
  A的期望收益率=10%+2*（14%-10%）=18%B的期望收益率=10%+1*（14%-10%）=14%C的期望收益率=10%+0.5（14%-10%）=12%该组合的期望收益率=60%*18%+30%*14%+10%*12%=16.2%预期收益也称为期望收益，是指如果没有意外事件发生时根据已知信息所预测能得到的收益。
通常未来的资产收益是不确定的。
不确定的收益可以用多种可能的取值及其对应的概率来表示，这两者的加权平均，即数学期望值，就是资产的预期收益。
  学习之前先来做一个小测试吧点击测试我合不合适学会计在投资理财中，预期收益的重要性，怎么强调都不为过。
它是进行投资决策的关键，输入变量计算。
不对它做出估计，什么买卖决策、投资组合一切都免谈。
它不仅对投资者重要，对于公司管理者来说，也同样重要，因为公司股票的预期收益是影响公司资本成本的主要因素，关系到公司将来选择什么样的投资项目。
学习财务知识可以到恒企教育，恒企教育在教辅交互上，应用大数据实践精准教育，真正实现个性化教育，建立有效的课前、课中、课后辅导标准体系，积极实践社群班级管理，让学员自觉形成自适应学习。

六、如何用回归直线法求资产的系统风险系数β

从本世纪七十年代以来，西方学者对CAPM进行了大量的实证检验。
这些检验大体可以分为三类： 1.风险与收益的关系的检验 由美国学者夏普（Sharpe）的研究是此类检验的第一例。
他选择了美国34个共同基金作为样本，计算了各基金在1954年到1963年之间的年平均收益率与收益率的标准差，并对基金的年收益率与收益率的标准差进行了回归，他的主要结论是： a、在1954—1963年间，美国股票市场的收益率超过了无风险的收益率。
 b、 基金的平均收益与其收益的标准差之间的相关系数大于0.8。
 c、风险与收益的关系是近似线形的。
 2.时间序列的CAPM的检验 时间序列的CAPM检验最著名的研究是Black，Jensen与Scholes在1972年做的，他们的研究简称为BJS方法。
BJS为了防止β的估计偏差，采用了指示变量的方法，成为时间序列CAPM检验的标准模式，具体如下： a、利用第一期的数据计算出股票的β系数。
 b、 根据计算出的第一期的个股β系数划分股票组合，划分的标准是β系数的大小。
这样从高到低系数划分为10个组合。
 c、采用第二期的数据，对组合的收益与市场收益进行回归，估计组合的β系数。
 d、 将第二期估计出的组合β值，作为第三期数据的输入变量，利用下式进行时间序列回归。
并对组合的αp进行t检验。
 其中：Rft为第t期的无风险收益率 Rmt为市场指数组合第t期的收益率 βp指估计的组合β系数 ept为回归的残差 BJS对1931—1965年间美国纽约证券交易所所有上市公司的股票进行了研究，发现实际的回归结果与理论并不完全相同。
BJS得出的实际的风险与收益关系比CAPM 模型预测的斜率要小，同时表明实际的αp在β值大时小于零，而在β值小时大于零。
这意味着低风险的股票获得了理论预期的收益，而高风险股票获得低于理论预测的收益。
 3.横截面的CAPM的检验 横截面的CAPM检验区别于时间序列检验的特点在于它采用了横截面的数据进行分析，最著名的研究是Fama和Macbeth（FM）在1973年做的，他们所采用的基本方法如下： a、根据前五年的数据估计股票的β值。
 b、 按估计的β值大小构造20个组合。
 c、计算股票组合在1935年—1968年间402个月的收益率。
 d、 按下面的模型进行回归分析，每月进行一次，共402个方程。
 Rp=g0+g1bp+g2bp2+g3sep+ep 这里：Rp为组合的月收益率、 βp为估计的组合β值 bp2为估计的组合β值的平方 sep为估计βp值的一次回归方程的残差的标准差 g0、g1、g2、g3为估计的系数，每个系数共402个估计值 e、对四个系数g0、g1、g2、g3进行t检验 FM结果表明： ①g1的均值为正值，在95%的置信度下可以认为不为零，表明收益与β值成正向关系 ②g2、g3在95%的置信度下值为零，表明其他非系统性风险在股票收益的定价中不起主要作用。
 1976年Richard·Roll对当时的实证检验提出了质疑，他认为：由于无法证明市场指数组合是有效市场组合，因而无法对CAPM模型进行检验。
正是由于罗尔的批评才使CAPM的检验由单纯的收益与系统性风险的关系的检验转向多变量的检验，并成为近期CAPM检验的主流。
最近20年对CAPM的检验的焦点不是 ，而是用来解释收益的其它非系统性风险变量，这些变量往往与公司的会计数据相关，如公司的股本大小，公司的收益等等。
这些检验结果大都表明：CAPM模型与实际并不完全相符，存在着其他的因素在股票的定价中起作用。

参考文档