怎么求股票a与b相关系数~怎么求 二次函数最低点最高点， 有公式吗

一、a=2022x2022x2022，b=2022x2022x2022求a与b的关系?

a-b=2022x2022x2022-2022x2022x2022=2022x2022>；
0所以a>；
b

二、如何分析两只股票的涨幅的相关系数？

首先你需要选择两只股票的涨跌数据，比如可以是向前为其三个月的数据，或者是一年的数据，然后把两只股票每天的涨跌数据 一一对应收集起来。
然后就可以采用简单的相关分析，甚至其他的统计分析方法分析两只股票的关系。
不过说实话 中国的股票数据反映的并不是经济规律的真相，更多的是政策和市场信息的影响。

三、已知两只股票相关系数为-1，如何求无风险利率，谢谢啦~~~

列两个方程组，可以参考无风险套利推导公式++

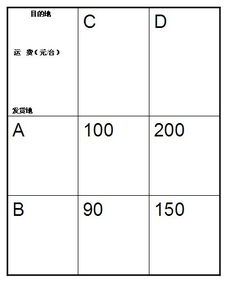
四、A市和B市分别有库存某种机器12台和6台，现决定支缓给C市10台和D市8台，

解 根据题意得：(1)Y＝300x＋500(6－x)＋400(10－x)＋800[12－(10－x)]＝200x＋8600．(2)因运费不超过9000元（你的题目给错了，不是900元，900块钱只够3台的运费）∴Y＝200x＋8600≤9000，解得x≤2．∵0≤x≤6，∴0≤x≤2．则x＝0，1，2，所以有三种调运方案．(3)∵0≤x≤2，且Y＝200x＋8600，∴当x＝0时，Y的值最小，最小值为8600元，此时的调运方案是：B市运至C市0台，运至D市6台，A市运往C市10台，运往D市2台，最低总运费为8600元．PS.这样的问题最好问问老师或者同学，当面讲就很容易理解。
如果直接拿答案来看的话，不好理解是一方面，另一方面可能下次碰到类似题目还是不会。

五、假设证券市场中有股票A和B，其收益和标准差如下表，如果两只股票的相关系数为-1。

这道题是希望通过运用两只股票构建无风险的投资组合，由一价原理，该无风险投资组合的收益就是无风险收益率。
何为无风险投资组合？即该投资组合收益的标准差为0，由此，设无风险投资组合中股票A的权重为w，则股票B的权重为（1-w），则有：{(5%w)^2+[10%(1-w)]^2+2*5%*10%(-1)(1-w)w}^(1/2)=0等式两边同时平方，并扩大10000倍（消除百分号），则有：25(w^2)+100(1-w)^2-100w(1-w)=0化简为：225w^2-300w+100=0(15w-10)^2=0 则w=2/3则，该投资组合的收益率为：2%*（2/3）+5%*（1/3）=9%/3=3%

六、百度 某投资者将一只股票加入到某组合中，如该股票与拟加入组合有相同标准差，且两者相关系数小

你指的是某股票与某组合之间的协方差吧？协方差=AB两组变量的相关性系数×A变量的标准差×B变量的标准差

七、怎么求 二次函数最低点最高点， 有公式吗

y=ax²+bx+ca>；
0时，有最低点。
x=-b/2a时，最低点为y=（4ac-b²）/4aa<；
0时，有最高点。
x=-b/2a时，最高点为y=（4ac-b²）/4a二次函数表达式为y=ax²+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。
如果令y值等于零，则可得一个二次方程。
该方程的解称为方程的根或函数的零点。
交点式为 ；
 ；
（仅限于与x轴有交点的抛物线），与x轴的交点坐标是 ；
 ；
和 ；
 ；
。
扩展资料：在平面直角坐标系中作出二次函数y=ax2+bx+c的图像，可以看出，在没有特定定义域的二次函数图像是一条永无止境的抛物线。
 如果所画图形准确无误，那么二次函数图像将是由 ；
平移得到的。
轴对称：二次函数图像是轴对称图形。
对称轴为直线 ；
对称轴与二次函数图像唯一的交点为二次函数图象的顶点P。
特别地，当b=0时，二次函数图像的对称轴是y轴（即直线x=0）。
a，b同号，对称轴在y轴左侧；
a，b异号，对称轴在y轴右侧。
当a>；
0，与b同号时（即ab>；
0），对称轴在y轴左；
 因为对称轴在左边则对称轴小于0，也就是- b/2a<；
0，所以 b/2a要大于0，所以a、b要同号当a>；
0，与b异号时（即ab<；
0），对称轴在y轴右。
因为对称轴在右边则对称轴要大于0，也就是- b/2a>；
0， 所以b/2a要小于0，所以a、b要异号可简单记忆为左同右异，即当对称轴在y轴左时，a与b同号（即a>；
0，b>；
0或a<；
0，b<；
0）；
当对称轴在y轴右时，a与b异号（即a0或a>；
0，b<；
0）（ab<；
0）。
参考资料：股票百科——二次函数

参考文档