勾3股4弦5怎么算直角.在施工中放线怎么利用勾三股四弦五才能放出直角线

一、我是木工放线时常用勾三股四弦五这个定理来求直角，问勾是1米股是2米

不可以  那只是直角三角形勾股定理的一个特例

二、在施工中放线怎么利用勾三股四弦五才能放出直角线

在直线AD为初始直线，以A点为起点向右量取300mm，即AB=300，以A点为圆心，400mm为半径画圆，以B点为圆心，500mm为半径画圆，两圆交于点C，连接AC，BC，则AC垂直于BC，完毕。

三、可以用“勾三，股四，弦五”的关系来求全部的直角三角形的“求第三遍”的问题吗？

不可以  那只是直角三角形勾股定理的一个特例

四、勾3股4弦5三角形的角度是多少？

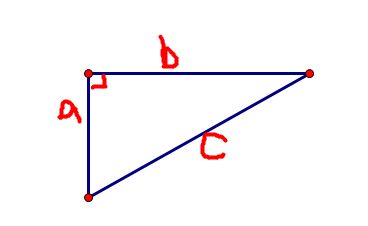
弦5相对着的角是90度，勾3的对角是37度，股4的对角为53度。
详细解释：首先由勾3股4弦5知三角形满足勾股定理，是直角三角形；
设勾3的对角是A，股4的对角为B。
那么sinA=3/5，A=arcsin3/5=37度。
sinB=4/5，B=arcsin4/5=53度。
扩展资料勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。
勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。
在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
参考资料来源：股票百科——勾股定理

五、勾3股4玄5的算计方法与公式

我们用勾（a）和股（b）分别表示直角三角形得到两条直角边，用弦（c）来表示斜边，则可得：勾2+股2=弦2亦即：a2+b2=c2 
勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年首先发现的。
其实，我国古代得到人民对这一数学定理的发现和应用，远比毕达哥拉斯早得多。
如果说大禹治水因年代久远而无法确切考证的话，那么周公与商高的对话则可以确定在公元前1100年左右的西周时期，比毕达哥拉斯要早了五百多年。
其中所说的勾3股4弦5，正是勾股定理的一个应用特例（32+42=52）。
所以现在数学界把它称为勾股定理，应该是非常恰当的。
 
在稍后一点的《九章算术一书》中，勾股定理得到了更加规范的一般性表达。
书中的《勾股章》说；
“把勾和股分别自乘，然后把它们的积加起来，再进行开方，便可以得到弦。
”把这段话列成算式，即为：弦=（勾2+股2）(1/2)亦即：c=（a2+b2）(1/2) 
中国古代的数学家们不仅很早就发现并应用勾股定理，而且很早就尝试对勾股定理作理论的证明。
最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽。
赵爽创制了一幅“勾股圆方图”，用形数结合得到方法，给出了勾股定理的详细证明。
在这幅“勾股圆方图”中，以弦为边长得到正方形ABDE是由4个相等的直角三角形再加上中间的那个小正方形组成的。
每个直角三角形的面积为ab/2；
中间懂得小正方形边长为b-a，则面积为（b-a）2。
于是便可得如下的式子：4×（ab/2）+（b-a）2=c2化简后便可得：a2+b2=c2亦即：c=（a2+b2）(1/2) 
赵爽的这个证明可谓别具匠心，极富创新意识。
他用几何图形的截、割、拼、补来证明代数式之间的恒等关系，既具严密性，又具直观性，为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。
以后的数学家大多继承了这一风格并且代有发展。
例如稍后一点的刘徽在证明勾股定理时也是用的以形证数的方法，只是具体图形的分合移补略有不同而已。

参考文档