无偏估计量怎么求例题相关股票；概率论与数理统计选择题，怎么求无偏估计

一、设总体x的概率密度为f(x)=2x/θ^2 求无偏估计

(1)矩估计θM=1.5X~ 是无偏估计。
(2)极大似然θL=max{X1，X2，X3，X4...Xn}。
EθL=Emax{X1，X2，X3，X4...Xn} 不是无偏估计。
估计量的数学期望等于被估计参数的真实值，则称此此估计量为被估计参数的无偏估计，即具有无偏性，是一种用于评价估计量优良性的准则。
无偏估计的意义是：在多次重复下，它们的平均数接近所估计的参数真值。
无偏估计常被应用于测验分数统计中。
扩展资料：用样本均值作为总体均值的估计时，虽无法说明一次估计所产生的偏差，但这种偏差随机地在0的周围波动，对同一统计问题大量重复使用不会产生系统偏差。
但是需要注意的是，所谓“平均为零”只有在大量重复使用此模型时才能体现出来。
关于这一点，需要用大数定律作进一步解释。
无偏估计并不总是存在的，如服从二项分布的总体B(n，p)，0<；
p<；
1，则1/p的无偏估计就不存在。
有时，无偏估计虽然存在，但不够合理。
又有些问题中，无偏估计很多，则其优良性由它们的方差来决定，方差越小越优良。
参考资料来源： 百科——无偏估计

二、无偏估计量判断：设总体X的均值为【0，a】上服从均匀分布，其中a>；0未知，则a的无偏估计量为

B. E(1/2X1+1/6X2+1/3X3)=E(1/2X1)+E(1/6X2)+E(1/3X3)=(1/2+1/6+1/3)a=a因此无偏于a

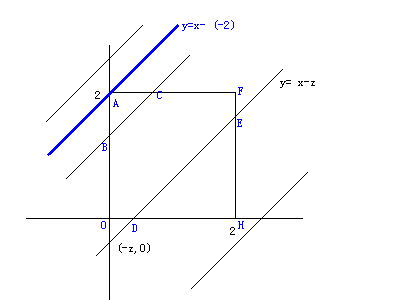
三、概率论与数理统计选择题，怎么求无偏估计

如果估计量的期望等于数复学期望E(X)，则这个估计量就是无偏制估计。
例如E(2X2-X4)=2E(X2)-E(X4)=2E(X)-E(X)=E(X)，所zhidao以B项是无偏估计。
而E(X1+X3-2X5)=E(X1)+E(X3)-2E(X4)=E(X)+E(X)-2E(X)=0≠E(X)，所以A项不是无偏估计，答案是A。

四、设?θ=?θ（X1，X2，…，Xn）是参数θ的一个估计量，若______，则称?θ是θ的无偏估计量

就是根据方差公式求的：D(aX+bY)=a²DX+b²DY      (X，Y独立）注：即使是D(aX-bY)，也是a²DX+b²DY

五、怎么算无偏估计量

用最大似然估计把θ^2的估计量算出来，然后验证一下它的期望是不是等于真值θ^2。

六、概率论无偏估计的有效性一题求教

就是根据方差公式求的：D(aX+bY)=a²DX+b²DY      (X，Y独立）注：即使是D(aX-bY)，也是a²DX+b²DY

参考文档