股票股利增长模型的方程怎么解固定股利增长模型里面，如果r（贴现率）小于或者等于g（股利增长率），那么贴现值怎么算？

一、股利固定增长模型中有一个公式：P=D0*(1+g)/(K-g)=D1/(K-g) 如何来决定哪种情况下是使用D0，情况下是使用D1.

看题中给的条件，D0是基期的，D1是第一年的，如果题中给出本年支付的股利数字，然后告诉你增长率，那么就要用D0，如果直接给出下一年的股利，就用D1.

二、下图是股利两阶段增长模型的折现值，求给后半部分的推导过程。

Vn=[D0(1+g)^n(1+gn)/(r-gn)] n时点未来鼓励价值Vn折现除以（1+r)^n

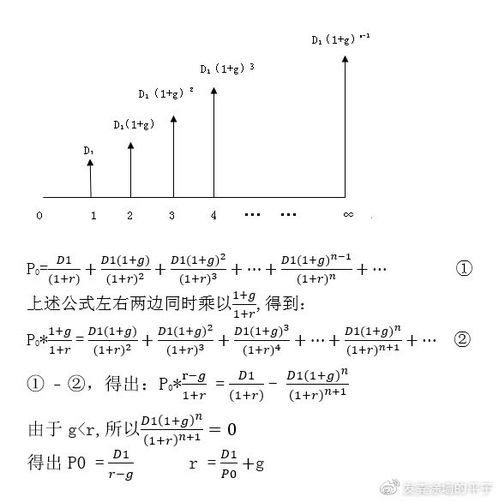
三、股利贴现模型这个等式怎么推导出来的？？？

这是等比数列求和，首项a1是D1/(1+K)，公比q是(1+g)/(1+K)，所以正无穷，因为假设里K>；
g，所以q^n=(1+g)^n/(1+K)^n=0，而分母里1-q=(K-g)/(1+K)所以得出D1/(K-g)

四、股利增长模型

【答案】BCD　　【解析】留存收益没有筹资费用，不需要考虑筹资费用率。
　　资本资产定价模型法　　Ks=Rs=RF+β（Rm-RF）　　风险溢价法　　Ks=Kb+RPc

五、股利增长模型中有一个公式：P=D0*(1+g)/(K-g)=D1/(K-g) 如何来决定哪种情况下是使用D0，情况下是使用D1

D0与D1只是基期不同，D0以前一年为增长点，D1以本年开始为增长点

六、固定股利增长模型里面，如果r（贴现率）小于或者等于g（股利增长率），那么贴现值怎么算？

股利折现模型有三个假设：1、股利支付是永久的；
2、股利增长率是永续的；
3、r>；
g。
最后之所以得到D/(r-g)，是带着r>；
g的假设，由无限期的等比数列推导而来的。
r<；
g时推导就不能这么推导了，要算PV只能直接逐期折现。
所以最后你会发现折现的结果是PV等于正无穷，显然不合逻辑。
所以要么g不可能一直那么高（从企业生命周期角度理解），要么r不可能一直那么低（从一般均衡角度理解），总之r<；
g不可能永远持续。

参考文档