股票动态规划算法有哪些--动态规划算法（pascal）

一、动态规划怎样计算最优解和最优值

动态规划算法通常用于求解具有某种最优性质的问题，需要最优子结构性质来确定最优策略。
一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。
简而言之，一个最优化策略的子策略总是最优的。
一个问题满足最优化原理又称其具有最优子结构性质。

二、会计指标中哪些是动态指标？哪些是静态指标？怎么区分的

动态指标就是反映在某一时期里所发生的某种变化情况，也可称时时期指标。
静态指标就是反映某一时点的某种状况，它所表示的是人口发展连续不断变化过程中的一个瞬间静止情况，通常称为时点指标。
只有这个数值还有时期数的话，那就说明这是一个动态指标，如销售、利润等。
而如果只是两个时点数得出的值的话，那就是一个静态指标，进点数主要是就是你在某个时间的数值，如资产、负债、存货等。
纠正一下的时，这两个指标不是会计指标，这两个指标是统计指标术语。

三、详解动态规划算法

其实你可以这么去想。
 能用动态规划解决的问题，肯定能用搜索解决。
 但是搜素时间复杂度太高了，怎么优化呢？ 你想到了记忆化搜索，就是搜完某个解之后把它保存起来，下一次搜到这个地方的时候，调用上一次的搜索出来的结果。
这样就解决了处理重复状态的问题。
 动态规划之所以速度快是因为解决了重复处理某个状态的问题。
 记忆化搜索是动态规划的一种实现方法。
 搜索到i状态，首先确定要解决i首先要解决什么状态。
 那么那些状态必然可以转移给i状态。
 于是你就确定了状态转移方程。
 然后你需要确定边界条件。
 将边界条件赋予初值。
 此时就可以从前往后枚举状态进行状态转移拉。

四、简述贪心，递归，动态规划，及分治算法之间的区别和联系

联系：都是问题求解之时的一种算法。
区别：一、作用不同1、贪心算法：把子问题的解局部最优解合成原来解问题的一个解。
2、递归算法：问题解法按递归算法实现。
如Hanoi问题；
数据的结构形式是按递归定义的。
如二叉树、广义表等。
3、动态规划：动态规划算法通常用于求解具有某种最优性质的问题。
4、分治算法：可以再把它们分成几个更小的子问题，以此类推，直至可以直接求出解为止。
二、方法不同1、贪心算法：在对问题求解时，总是做出在当前看来是最好的选择。
也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。
2、递归算法：通过重复将问题分解为同类的子问题而解决问题。
3、动态规划：将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。
4、分治算法：将一个规模为N的问题分解为K个规模较小的子问题。
三、特点不同1、贪心算法：根据题意选取一种量度标准。
2、递归算法：递归就是在过程或函数里调用自身。
3、动态规划：虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时间无关的静态规划(如线性规划、非线性规划)，只要人为地引进时间因素，把它视为多阶段决策过程，也可以用动态规划方法方便地求解。
4、分治算法：原问题可以分解为多个子问题；
原问题在分解过程中，递归地求解子问题；
在求解并得到各个子问题的解后。

五、动态规划算法的题目（急）

给出个思路吧：阶段变量i：1~n门课程状态变量h：已经用掉的小时数h决策变量dh：下一门课程分配的小时数dh目标函数sum_f：已经在前i门课上取得的总成绩sum_f状态转移方程：sum_f(i+1)=sum_f(i)+f(i+1)顺时序递推计算即可.

六、怎么用动态规划法求斐波那契数列

我不会乱说动态规划=递推=[F(n)=F(n-1)+F(n-2)]的就算有动规也是O(n)要优化出门右转矩阵乘法O(log2n)

七、PASCAL中什么是动态规划

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。
1957年出版了他的名著Dynamic Programming，这是该领域的第一本著作。

动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。
例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法比用其它方法求解更为方便。

虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时间无关的静态规划(如线性规划、非线性规划)，只要人为地引进时间因素，把它视为多阶段决策过程，也可以用动态规划方法方便地求解。
 
动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。
不象前面所述的那些搜索或数值计算那样，具有一个标准的数学表达式和明确清晰的解题方法。
动态规划程序设计往往是针对一种最优化问题，由于各种问题的性质不同，确定最优解的条件也互不相同，因而动态规划的设计方法对不同的问题，有各具特色的解题方法，而不存在一种万能的动态规划算法，可以解决各类最优化问题。
因此读者在学习时，除了要对基本概念和方法正确理解外，必须具体问题具体分析处理，以丰富的想象力去建立模型，用创造性的技巧去求解。
我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论，逐渐学会并掌握这一设计方法。

八、动态规划算法（pascal）

在计算够不够开销时 20%这个数据是废的 你可以先减去预算再考虑存多少钱 比如手头钱的数目为a 预算为b 存在妈妈处的钱为c 可以先从a中减去b 然后c就等于c+a div 100 *100 var 略 begin a：=0；
 c：=0；
 bo：=true；
 for i：=1 to 12 do begin read(b[i])；
 inc(a，300)；
 if a

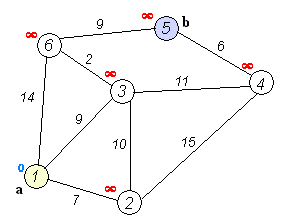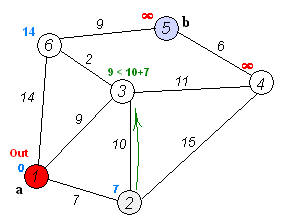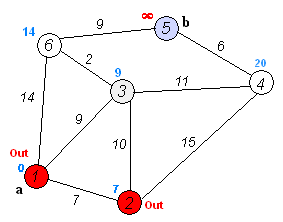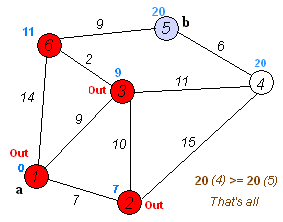
九、动态规划和贪心算法是什么？？

给出个思路吧：阶段变量i：1~n门课程状态变量h：已经用掉的小时数h决策变量dh：下一门课程分配的小时数dh目标函数sum_f：已经在前i门课上取得的总成绩sum_f状态转移方程：sum_f(i+1)=sum_f(i)+f(i+1)顺时序递推计算即可.

参考文档