量纲不同如何比较：量纲的国际标准

一、单位和量纲有何区别

单位是由量纲组成的。
现在有7种基本量纲：长度、质量、时间、温度、电流、发光强度、物质的量。
这7个量纲之间没有任何关系，但相互组合就会弄出各种不同的单位来。
比如速度=长度/时间，密度=质量/长度^3，电阻=（质量*长度^2）/（时间*电流^2）。
就是说速度的量纲是由长度的量纲除以时间的量纲得来的。
懂了吧！分就给我吧~

二、具有相同量纲的量是否是同一量？相同的量是否具有相同的量纲？

1.相同的量可以有不同的量纲。
由于选取的基本量不同，同一个量在不同单位制里的量纲可以不同。
如码可以做为长度单位也可以做为速度单位。
2.具有相同量纲的量不一定是同一量。
量纲为1的量不一定是同一个量

三、为什么磁感应强度和磁场强度的基本物理量纲不同，分别

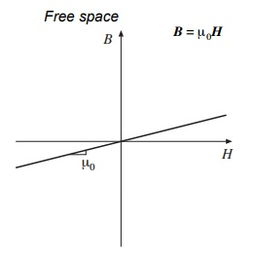
外加磁场在空间某处对物件的磁场作用程度，用磁场强度H表示。
外加磁场在空间某处对物件磁化后，并且物件磁化后感生一个自身磁场，此时物件的磁场作用为外加磁场与自身感生磁场的矢量和，这个矢量和恰好是外加磁场强度的μ （磁导率）倍，这个磁场矢量和作用用感应磁场强度B表示。
只有磁场中存在物件（介质）才有磁感应强度。
只有磁场，没有介质，磁场作用为磁场强度。

四、什么是量纲？力量系统和质量系统的基本量纲组合分别是怎样的

什么是量纲？力量系统和质量系统的基本量纲组合分别是怎样的？ ；
答：量纲的概念是在研究物理量的数量关系时产生的，它说明量测物理量时所用单位的性质。
力量系统的基本量纲组合是长度、时间、力。
质量系统的基本量纲组合是长度、时间、质量。

五、量纲的国际标准

按照国际标准，物理量Q的量纲记为dimQ，国际物理学界沿用的习惯记为[Q]。
量纲是物理学中的一个重要概念。
可以定性地表示出导出量与基本量之间的关系；
可以有效地进行单位换算；
可以检查物理公式的是否正确；
可以推知某些物理规律。
“在量制中，以基本量的幂的乘积表示该量制中一个量的表达式，这个表达式就是该量的量纲。
” 物理量之间的有规律联系还通过描述自然规律的各种定律表示出来。
因此当一个单位制的基本量确定后，其他的物理量就可以通过既定的关系或定律，定义为用基本量表示的导出量，并通过代数式表示为基本量的幂次乘积。
由于选取的基本量不相同，同一个物理量在不同的单位制里的量纲可以互不相同。
这在电磁学中是常有的。
例如高斯单位制中的基本量是长度、质量和时间，而电磁学的MKSA制（电磁单位制）中的基本量是长度、质量、时间和电流。
物理量之间的一定组合，使其量纲积内基本量的量纲指数均为零，称为无量纲积或无量纲物理量，有时也称为量纲为1的量。
例如应变dl/l的量纲dim(dl/l)=LL－1=1；
雷诺数Re=vlρ/μ，其中v、ρ、μ分别是流体的速率、密度和粘滞率；
l是物体或容器的特征线度，显然有dimRe=LT－1·L·ML－3·M－1LT=M0L0T0=1无量纲量的量纲为1，所以它的数值与所选用的单位制无关，用纯数表示。
任一合理构成的物理方程中的各项，都具有相同的量纲。
显然，量纲一致的方程的形式，不会因基本量的单位不同而改变。
在量纲分析中把一组无量纲积称为完全系 。
在国际单位制（SI）中，七个基本物理量长度、质量、时间、电流、热力学温度、物质的量、发光强度的量纲符号分别是L、M、T、I、Θ、N和J 。
例如：速度 v=ds/dt 量纲：LT－1加速度 a=dv/dt 量纲：LT－2力 F=ma 量纲：MLT－2压强 P=F/S 量纲：MLT－2L－2= MT－2L－1量纲是检查公式推导过程中是否准确的判据，虽然不能保证其正确，但可以找到错误。
一个物理理论通常由以下几个部分组成：概念，通常是抽象的，不能直接感知；
关于这些概念的数学表示（物理量）：假定一个或一组方程，表示物理量之间的关系。
在这一部分中，量纲扮演着重要角色。
采用不同的量制，同一物理量会有不同的量纲。
如表示电磁量的量制，历史上曾有CGSE和CGSM及SI等量制，对这几种量制之间，同一物理量的数值可以进行换算。
为了便于文献和书刊中的测量值之间的比较，多数科学家均采用国际单位制，但在某些专门领域，还保留了采用传统因袭的量制来表示 。
  国际制基本单位物理量名称物理量符号单位名称符号长度  L  米  m  质量  m  千克（公斤）  Kg  时间  t  秒  s  电流  Ι  安（安培）  A  热力学温度  T  开（开尔文）  K  物质的量  n（ν）  摩（摩尔）  mol  发光强度  I（Iv）  坎（坎德拉）  cd  注：1. 人们生活和贸易中，质量可能误认为是重量，实际上重量是由于重力而产生的，而质量是物质的性质。
2.单位符号一栏，前为中文符号，后为国际符号。
例：“安培”可简称“安”，也作为中文符号使用。
圆括号内的字，为前者的同义语。
例：“千克”也可成为“公斤”3.Kg(Kilogram) 原名称 G(Grave)。

六、不同种类的物理量是不能相加减，也不能列成等式或比较它们的大小这句话对吗？怎么理解不同种类物理量，动

所谓的不同种类，一般会有不同的单位，你能想象不同的单位相加吗？比方说，1人民币+1米是啥？没有意义……至于动量和冲量，它们的单位其实是一致的，即1kg·m/s=1N·s=1kg·m/s^2 ·s。
话又说回来，单位相同就能相加吗？未必。
1m身高+1m水深是啥？也是无意义的。
冲量和动量能相加，是因为有冲量定理：系统动量的增加等于系统合外力的冲量之和。
这个定理是由牛顿三定律保证的。
但也不意味着系统A的动量和系统B的冲量可以相加——你得有物理意义啊！此外，不同单位有时可以相乘，你可以理解吧？

七、量纲的国际标准

八、量纲的量纲分析

量纲分析（dimensional analysis）是对物理现象或问题所涉及的物理量的属性进行分析，从而建立因果关系的方法。
量纲分析是自然科学中一种重要的研究方法，它根据一切量所必须具有的形式来分析判断事物间数量关系所遵循的一般规律。
通过量纲分析可以检查反映物理现象规律的方程在计量方面是否正确，甚至可提供寻找物理现象某些规律的线索。
客观规律要求数值的非实质变化必须保证事物客观大小的绝对性。
具体说，任何两个一定大小的同类量，不论测量的单位如何，它们的相对大小永远不变，即它们的比值对任何单位都必须是个定值。
同类量相对大小对于单位的不变性是度量的根本原则。
违反这一原则，量度将没有任何意义。
根据这个原则，可以导出以下的重要结论：在确定的单位制中，所有物理量的量纲都具有基本量量纲的幂次积形式（证明从略）。
实际现象总是同时参有许多物理量。
它们间通过理论与实验建立起一定的依存关系，构成某一客观规律的数学算式。
显然，这种数量关系必须有具体内容，列成算式时要首先考虑运算的含义。
物理中只有同类量或它们的同样组合才能进行加减。
另外，在建立算式时要采用统一单位制的观点，否则将无法按名数的大小来进行比较。
当然，单位总可以通过换算给予统一，因而不构成任何限制。
其次，所建立反映客观实际规律的关系式，必须在单位尺度的主观任意变换下不受破坏。
关系式的这一性质称为“完整性”。
表现数量关系的最一般形式是多项式。
保证多项式的完整性有两种办法：一是要求出现在算式中的一切参量都是无量纲纯数，二是要求式中所有各项具有完全相同的量纲，也就是每一项的每一基本量纲都有相同的幂次，即所谓量纲的齐次性。
算式中各项都是有关名数的幂次积，它们可分为量数和量纲两部分。
既然量纲齐次，等式两边的量纲因子就可以相消，只剩下纯粹由量数构成的关系方程，也就是无量纲化了。
总之，量纲齐次是构成完整性的充分和必要条件。
应该指出，任何两个量纲齐次的算式，假如硬性相加成为新的多项式，它虽然仍具有完整性，但可能变为非量纲齐次。
这是因为两个算式分别表示不同类量间的关系。
任何算式应用于具体实例都是如此，所以无需看作是量纲齐次的破坏。
所谓量纲独立指其中任何一个量的量纲式不能由其余量的量纲式的幂次积所组成。
例如MLT体系中长度[L]、速度[LT－1]和能量[ML2T－2]三者是独立的，而长度[L]、速度[LT－1]和加速度[LT－2]三者间则非独立的。
三个基本量的体系一般也只具有不多于三个的量纲独立量 。
历史上最早把物理量的属性看作物理量量纲的是J.傅里叶。
他把dimension一词的概念，从几何学中的长度、面积和体积的范畴，推广到物理学中的长度、时间、质量、力、能、热等物理量的范畴，这一词不再限于长、宽、高等几何空间的属性，而泛指物理现象中物理量的属性，称之为量纲。
他说换了单位不仅某量的大小变了，与该量有关的量的大小也跟着变。
 　　在同一个时期，O.雷诺和瑞利应用量纲的概念屡屡取得成功。
雷诺首先用于检验方程各项的齐次性。
瑞利则用于克服求解问题中遇到的数学困难。
后来，E.白金汉提出：每一个物理定律都可以用几个零量纲幂次的量（称之为Π）来表述。
P.布里奇曼将白金汉的提法称之为Π定理。
实际上，傅里叶早已指明这种提法的实质，只可惜在他那个年代并没有引起大家的重视 。
量纲分析又叫因次分析，是20世纪初提出的在物理领域中建立数学模型的一种方法。
量纲分析就是在量纲法则的原则下，分析和探求物理量之间关系。
量纲分析的基础是量纲法则。
而在深层次运用中，会运用到Π定理，以至于有时把量纲分析直接看作“运用Π定理进行无量纲化的过程”。

参考文档